Rekenen met plaatjes – Een Bayesiaanse kijk op steekproefcontrole
De basis voor dit Bayesiaanse model is te vinden in het proefschrift: “A Bayesian Audit Assurance Model with Application to the Component Materiality Problem in Group Audits” (Stewart, T.R. 2013) en in een artikel in de Accounting Review: http://ssrn.com/abstract=2142891
Het vernieuwende van de manier waarop hier is gekeken naar steekproeven is dat we niet meer rekenen met schattingen zoals de geprojecteerde fout en de maximale fout, maar naar de gehele kansverdeling van die fout: welk bedrag aan fouten in de te controleren of gecontroleerde populatie heeft welke kans? Die aanpak is essentieel voor Bayesiaanse statistiek: we nemen aan dat de onbekende fout in een populatie een kansverdeling heeft. In dit onderzoek is een Gammaverdeling verondersteld, mede omdat die verdeling mooi aansluit bij de Poisson verdeling voor het aantal fouten in een steekproef die uit die populatie kan worden getrokken, en die de basis is voor de bekende tabel met R waarden (of S waarden bij SRA accountantskantoren).

(1893-1976)
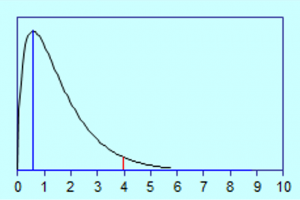
We zien hier een populatie met een geprojecteerde (meest waarschijnlijke) fout van ongeveer 0,6 (miljoen euro) en een 95% betrouwbare maximale fout van bijna 4 (miljoen euro). Het eerste zien we aan de top van de curve, het tweede zien we doordat er 5% oppervlakte rechts van het rode streepje ligt. Zo’n plaatje kan een steekproefresultaat zijn, maar kan ook een inschatting van de accountant zijn op basis van risicoanalyse, de beoordeling van de AO/IB, of ervaringen uit het verleden.
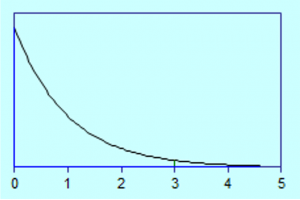
Als voorbeeld: een steekproef van 100 uit een massa van 1 miljoen euro geeft bij 0 fouten een geprojecteerde fout 0 en een 95% betrouwbare maximale fout van 30.000 (links) en bij 1 fout een geprojecteerde fout 10.000 en een 95% betrouwbare maximale fout van 47.500 (rechts).
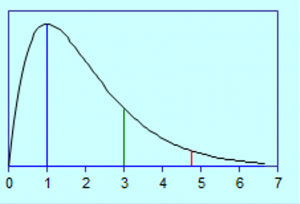
Het interessante van deze plaatjes is dat er als het ware mee gerekend kan worden. Voor het wiskundige bewijs zie het artikel of het proefschrift. Optellen en aftrekken, vermenigvuldigen, delen…..
Natuurlijk zijn er bij dat rekenen voorwaarden te stellen waaronder de uitkomsten beter of juist minder goed passen. Hoe groter bijvoorbeeld het verschil tussen de omvang van twee populaties des te minder exact zullen de resultaten van deze berekeningen zijn. Maar, het gaat nu om het principe en niet om de details.
Bijvoorbeeld:
1. Ik heb een plaatje voor massa 1 en een plaatje voor massa 2. Hoe ziet het plaatje er uit als ik die massa’s samenvoeg? Dit slaat op het geven van één oordeel over het totaal van 2 of meer heterogene massa’s.

Merk op dat de geprojecteerde fout per massa 0 is maar voor het totaal niet; dat is het aggregatierisico uit COS 600, 21c. Voor statistici is dit vanzelfsprekend: de centrale limietstelling geeft aan dat het optellen van onafhankelijke kansverdelingen uiteindelijk leidt tot een (symmetrische) normale verdeling.
2. Ik weet aan welk plaatje de totale massa moet voldoen. Wat zijn de beste plaatjes voor delen 1 en 2 die optellen tot het gewenste plaatje?
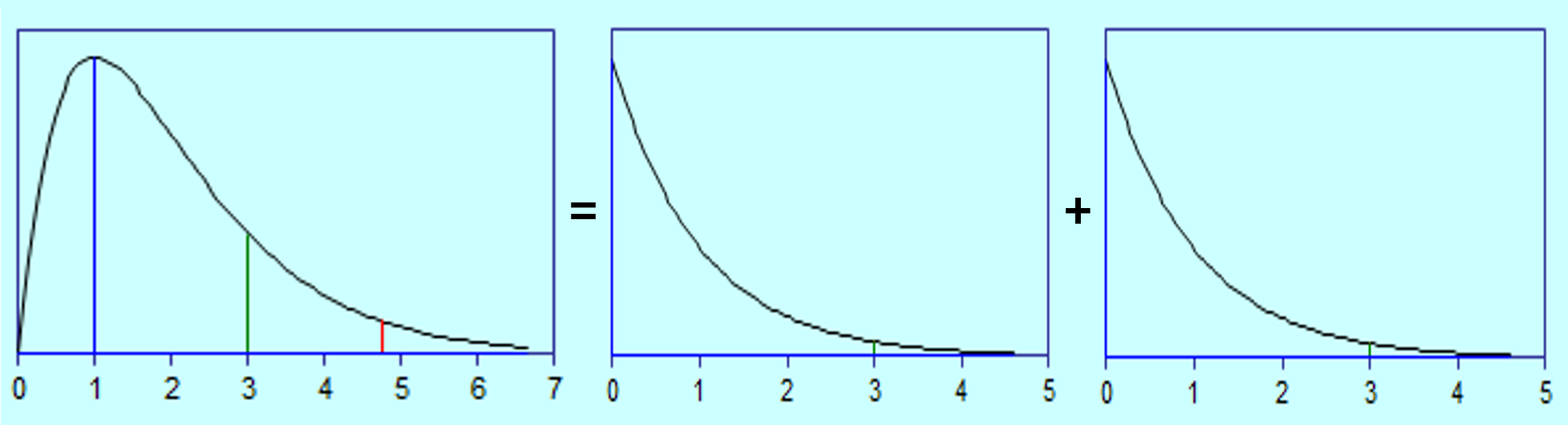
Dit is het toerekenen van de materialiteit naar heterogene deelpopulaties: het bepalen voor de materialiteit voor een groepsonderdeel (COS 600, 21c en A43) of van de uitvoeringsmaterialiteit (COS 320, 9 en A12). Het nut van dit opdelen is dat fouten per deelpopulatie geëvalueerd kunnen worden.
Er bestaan oneindig veel antwoorden op de vraag welke twee plaatjes optellen tot een gegeven plaatje, maar het bijzondere van het proefschrift is dat daar is berekend wat de beste keuze is gegeven een gekozen criterium zoals de totale steekproefomvang of de totale controlekosten.
3. Vervolgens kunnen we ook vermenigvuldigen:
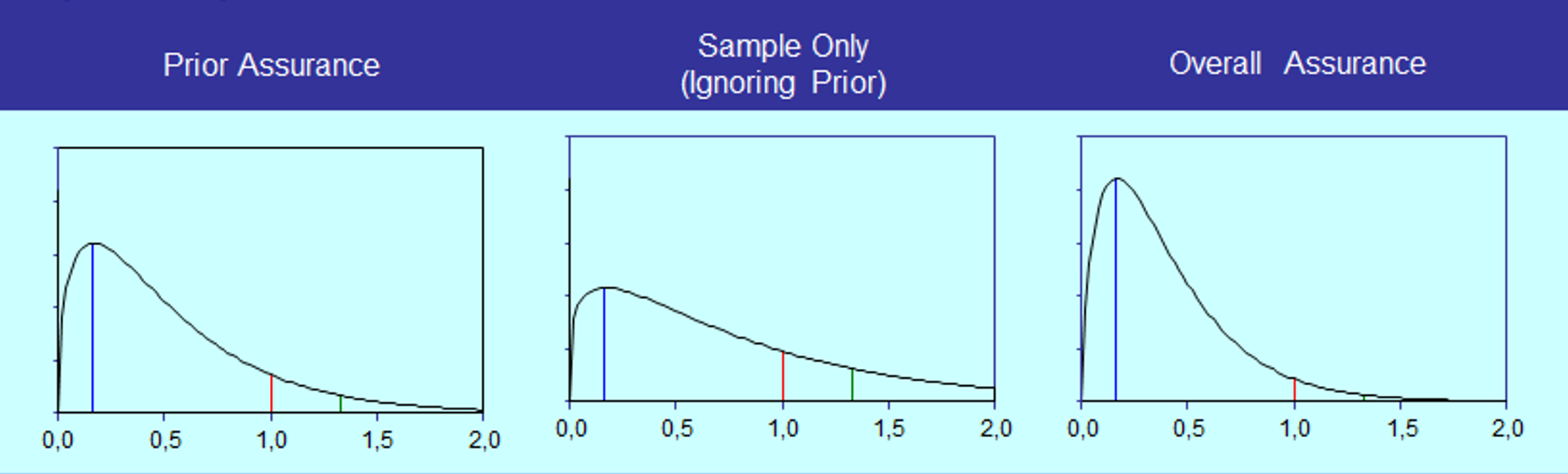
Dit is het Audit Risk Model 2.0: de accountant veronderstelt het linker plaatje en berekent hoeveel waarnemingen met hoeveel fouten leiden tot het gewenste rechterplaatje. Het klassieke model werkt alleen bij het veronderstellen en vinden van 0 fouten; nu kan ook voorkennis leiden tot efficiëntere steekproeven als een geprojecteerde fout vooraf wordt verondersteld. Deze convolutie van de Gammaverdeling is standaard in de Bayesiaanse statistiek.
4. Ten slotte kunnen we ook delen: dat is van toepassing als een homogene massa op verschillende plaatsen wordt verantwoord. Dan bepalen we de voorkennis voor de deelmassa die volgt uit de controle op de gehele massa. Het eindplaatje van de 3 plaatjes hiervoor voor de gehele populatie levert een beginplaatje voor eenzelfde analyse voor een deelpopulatie. Ook hier geldt natuurlijk dat wordt aangenomen dat de fout in de deelpopulatie weer een gammaverdeling volgt. Belangrijk daarbij is dat de deelpopulatie niet te klein mag zijn ten opzichte van de gehele populatie.
Voorbeeld van een toepassing van deze methode is een Shared Services Center waar transacties worden afgehandeld die later in verschillende verantwoordingen terechtkomen. Per verantwoording is een materialiteit gesteld, maar de controle zou efficiënter op de gehele populatie kunnen worden uitgevoerd.
